https://github.com/suncaiyu/LearnOpenGLCN

向量

向量与标量运算

标量(Scalar)只是一个数字（或者说是仅有一个分量的向量）。当把一个向量加/减/乘/除一个标量，我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
$$\begin{pmatrix}
\color{red}1\\
\color{green}2\\
\color{blue}3\\
\end{pmatrix}
+x =
\begin{pmatrix}
\color{red}1+\color{black}x\\
\color{green}2+\color{black}x\\
\color{blue}3+\color{black}x\\
\end{pmatrix}$$

向量取反

对一个向量取反(Negate)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了（或者说用-1数乘该向量）

$$-\overline{v}=-\begin{pmatrix}
\color{red}v_x\\
\color{green}v_y\\
\color{blue}v_z\\
\end{pmatrix}=
\begin{pmatrix}
\color{red}-v_x\\
\color{green}-v_y\\
\color{blue}-v_z\\
\end{pmatrix}$$

向量加减

$$\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + \bar{k} = \begin{pmatrix} \color{red}1 + \color{red}4 \\ \color{green}2 + \color{green}5 \\ \color{blue}3 + \color{blue}6 \end{pmatrix} = \begin{pmatrix} \color{red}5 \\ \color{green}7 \\ \color{blue}9 \end{pmatrix}$$

向量v = (4, 2)和k = (1, 2)可以直观地表示为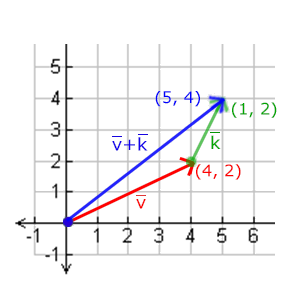： 就像普通数字的加减一样，向量的减法等于加上第二个向量的相反向量：

$$\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + -\bar{k} = \begin{pmatrix} \color{red}1 + (-\color{red}{4}) \\ \color{green}2 + (-\color{green}{5}) \\ \color{blue}3 + (-\color{blue}{6}) \end{pmatrix} = \begin{pmatrix} -\color{red}{3} \\ -\color{green}{3} \\ -\color{blue}{3} \end{pmatrix}$$

两个向量的相减会得到这两个向量指向位置的差。这在我们想要获取两点的差会非常有用。

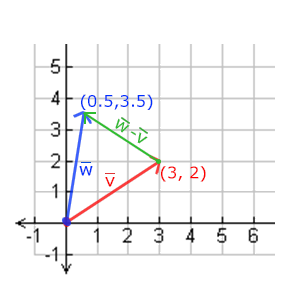
长度

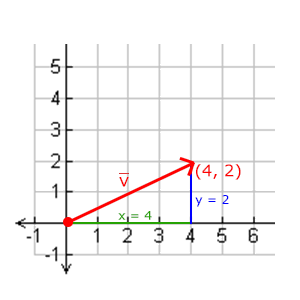因为两条边（x和y）是已知的，如果希望知道斜边v¯的长度，我们可以直接通过勾股定理来计算： $$||\color{red}{\bar{v}}|| = \sqrt{\color{green}x^2 + \color{blue}y^2}$$ ||v¯||表示向量v¯的长度，我们也可以加上z2把这个公式拓展到三维空间。

向量相乘

点乘 两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。可能听起来有点费解，我们来看一下公式：$$\bar{v} \cdot \bar{k} = ||\bar{v}|| \cdot ||\bar{k}|| \cdot \cos \theta$$ 所以，我们该如何计算点乘呢？点乘是通过将对应分量逐个相乘，然后再把所得积相加来计算的。两个单位向量的（你可以验证它们的长度都为1）点乘会像是这样：

$$\begin{pmatrix} \color{red}{0.6} \\ -\color{green}{0.8} \\ \color{blue}0 \end{pmatrix} \cdot \begin{pmatrix} \color{red}0 \\ \color{green}1 \\ \color{blue}0 \end{pmatrix} = (\color{red}{0.6} * \color{red}0) + (-\color{green}{0.8} * \color{green}1) + (\color{blue}0 * \color{blue}0) = -0.8$$

要计算两个单位向量间的夹角，我们可以使用反余弦函数cos−1 ，可得结果是143.1度。现在我们很快就计算出了这两个向量的夹角。点乘会在计算光照的时候非常有用。

    acos(-0.8) * 180 / 3.14.5926; // = 143.1

叉乘 叉乘只在3D空间中有定义，它需要两个不平行向量作为输入，生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘之后将会产生3个互相正交的向量。接下来的教程中这会非常有用。下面的图片展示了3D空间中叉乘的样子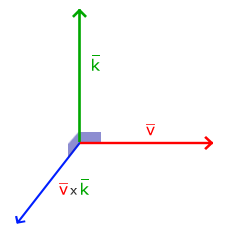： 不同于其他运算，如果你没有钻研过线性代数，可能会觉得叉乘很反直觉，所以只记住公式就没问题啦（记不住也没问题）。下面你会看到两个正交向量A和B叉积：

$$\begin{pmatrix} \color{red}{A_{x}} \\ \color{green}{A_{y}} \\ \color{blue}{A_{z}} \end{pmatrix} \times \begin{pmatrix} \color{red}{B_{x}} \\ \color{green}{B_{y}} \\ \color{blue}{B_{z}}  \end{pmatrix} = \begin{pmatrix} \color{green}{A_{y}} \cdot \color{blue}{B_{z}} - \color{blue}{A_{z}} \cdot \color{green}{B_{y}} \\ \color{blue}{A_{z}} \cdot \color{red}{B_{x}} - \color{red}{A_{x}} \cdot \color{blue}{B_{z}} \\ \color{red}{A_{x}} \cdot \color{green}{B_{y}} - \color{green}{A_{y}} \cdot \color{red}{B_{x}} \end{pmatrix}$$

是不是看起来毫无头绪？不过只要你按照步骤来了，你就能得到一个正交于两个输入向量的第三个向量。

矩阵

矩阵的加减

矩阵与标量之间的加减定义如下：

$$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \color{green}3 = \begin{bmatrix} 1 + \color{green}3 & 2 + \color{green}3 \\ 3 + \color{green}3 & 4 + \color{green}3 \end{bmatrix} = \begin{bmatrix} 4 & 5 \\ 6 & 7 \end{bmatrix}$$

矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算，所以总体的规则和与标量运算是差不多的，只不过在相同索引下的元素才能进行运算。这也就是说加法和减法只对同维度的矩阵才是有定义的。一个3×2矩阵和一个2×3矩阵（或一个3×3矩阵与4×4矩阵）是不能进行加减的。我们看看两个2×2矩阵是怎样相加的：

$$\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} + \begin{bmatrix} \color{red}5 & \color{red}6 \\ \color{green}7 & \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 + \color{red}5 & \color{red}2 + \color{red}6 \\ \color{green}3 + \color{green}7 & \color{green}4 + \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}6 & \color{red}8 \\ \color{green}{10} & \color{green}{12} \end{bmatrix}$$

矩阵的数乘

$$\color{green}2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} \color{green}2 \cdot 1 & \color{green}2 \cdot 2 \\ \color{green}2 \cdot 3 & \color{green}2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}$$

矩阵的相乘

1. 只有当左侧矩阵的列数与右侧矩阵的行数相等，两个矩阵才能相乘。
2. 矩阵相乘不遵守交换律(Commutative)，也就是说A⋅B≠B⋅A。 我们先看一个两个2×2矩阵相乘的例子：

$$\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} \cdot \begin{bmatrix} \color{blue}5 & \color{purple}6 \\ \color{blue}7 & \color{purple}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot \color{blue}5 + \color{red}2 \cdot \color{blue}7 & \color{red}1 \cdot \color{purple}6 + \color{red}2 \cdot \color{purple}8 \\ \color{green}3 \cdot \color{blue}5 + \color{green}4 \cdot \color{blue}7 & \color{green}3 \cdot \color{purple}6 + \color{green}4 \cdot \color{purple}8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}$$

矩阵的乘法是一系列乘法和加法组合的结果，它使用到了左侧矩阵的行和右侧矩阵的列。我们可以看下面的图片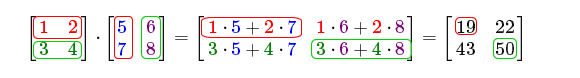： 我们首先把左侧矩阵的行和右侧矩阵的列拿出来。这些挑出来行和列将决定我们该计算结果2x2矩阵的哪个输出值。如果取的是左矩阵的第一行，输出值就会出现在结果矩阵的第一行。接下来再取一列，如果我们取的是右矩阵的第一列，最终值则会出现在结果矩阵的第一列。这正是红框里的情况。如果想计算结果矩阵右下角的值，我们要用第一个矩阵的第二行和第二个矩阵的第二列（译注：简单来说就是结果矩阵的元素的行取决于第一个矩阵，列取决于第二个矩阵）。

计算一项的结果值的方式是先计算左侧矩阵对应行和右侧矩阵对应列的第一个元素之积，然后是第二个，第三个，第四个等等，然后把所有的乘积相加，这就是结果了。现在我们就能解释为什么左侧矩阵的列数必须和右侧矩阵的行数相等了，如果不相等这一步的运算就无法完成了！

结果矩阵的维度是(n, m)，n等于左侧矩阵的行数，m等于右侧矩阵的列数。

如果在脑子里想象出这一乘法有些困难，别担心。不断地动手计算，如果遇到困难再回头看这页的内容。随着时间流逝，矩阵乘法对你来说会变成很自然的事。 我们用一个更大的例子来结束对矩阵相乘的讨论。试着使用颜色来寻找规律。作为一个有用的练习，你可以试着自己解答一下这个乘法问题，再将你的结果和图中的这个进行对比（如果用笔计算，你很快就能掌握它们）。

$$\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix}
 \\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}$$

矩阵与向量相乘

单位矩阵

在OpenGL中，由于某些原因我们通常使用4×4的变换矩阵，而其中最重要的原因就是大部分的向量都是4分量的。我们能想到的最简单的变换矩阵就是单位矩阵(Identity Matrix)。单位矩阵是一个除了对角线以外都是0的N×N矩阵。在下式中可以看到，这种变换矩阵使一个向量完全不变：

$$\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot 1 \\ \color{green}1 \cdot 2 \\ \color{blue}1 \cdot 3 \\ \color{purple}1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$$

缩放

我们下面会构造一个变换矩阵来为我们提供缩放功能。我们从单位矩阵了解到，每个对角线元素会分别与向量的对应元素相乘。如果我们把1变为3会怎样？这样子的话，我们就把向量的每个元素乘以3了，这事实上就把向量缩放3倍。如果我们把缩放变量表示为(S1,S2,S3)我们可以为任意向量(x,y,z)定义一个缩放矩阵：

$$\begin{bmatrix} \color{red}{S_1} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{S_2} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}{S_3} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{S_1} \cdot x \\ \color{green}{S_2} \cdot y \\ \color{blue}{S_3} \cdot z \\ 1 \end{pmatrix}$$

注意，第四个缩放向量仍然是1，因为在3D空间中缩放w分量是无意义的。w分量另有其他用途，在后面我们会看到。

位移

位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程，从而在位移向量基础上移动了原始向量。我们已经讨论了向量加法，所以这应该不会太陌生。

和缩放矩阵一样，在4×4矩阵上有几个特别的位置用来执行特定的操作，对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz)，我们就能把位移矩阵定义为：

$$\begin{bmatrix}  \color{red}1 & \color{red}0 & \color{red}0 & \color{red}{T_x} \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}{T_y} \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}{T_z} \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{red}{T_x} \\ y + \color{green}{T_y} \\ z + \color{blue}{T_z} \\ 1 \end{pmatrix}$$